Introduction

Nous pouvons déjà traduire "amélioration de la qualité d'une image numérique" par "réhaussement d'image numérique".

Comme vu durant le cours, l’imagerie numérique est utilisée dans de nombreux domaines comme l’imagerie médicale, satellitaire ou encore industrielle. Dans la plupart de ces domaines, les images obtenues sont de mauvaise qualité ou de qualités insuffisantes. En effet ces images peuvent subir des dégradations comme du bruit ou encore des distorsions.

Le rehaussement d’image intervient donc pour rendre ces images plus compréhensible et donc plus interprétable par l’œil humain. Le rehaussement a pour objectif de compenser les différentes dégradations qu’a pu subir l’image, afin de retrouver l’image d’origine ou alors d’amélioré certains détails de l’image.

Principe

Il existe différentes méthodes afin d’améliorer la qualité d’une image. Il y a des méthodes qui passe par le filtrage, d’autre par le calcul d’histogramme ou encore par l’amélioration du rapport image/bruit. Ces méthodes doivent être utilisées en fonction de ce que l’on veut obtenir. En effet chacune de ces méthodes aurait un effet bien spécifique sur l’image que se soit pour augmenter les contrastes ou bien mettre en avant des petits détails de l’image.

Nous allons maintenant voir le fonctionnement des ces diverses méthodes ainsi que les résultats que l’on obtient pour chacune.

Amélioration du rapport image/bruit

Cette méthode permet de diminuer le bruit dans une image. La technique consiste à prendre plusieurs fois l’image d’un même point de vue. On obtient donc n*l’image avec n*du bruit.

Ensuite il suffit d’appliquer un algorithme qui supprime les pixels différents entre chaque image et qui garde les pixels identiques. En effet, ces algorithmes se base sur le fait que le bruit est différent à chaque prise tandis que l’image, elle, est identique.

Amélioration par histogramme

Généralité sur les histogrammes

Qu'est ce qu'un histogramme ?

Un histogramme est un graphique statistique permettant de représenter la distribution des intensités des pixels d'une image, c'est-à-dire le nombre de pixels pour chaque intensité lumineuse. Un histogramme représente le niveau d'intensité en abscisse en allant du plus foncé (à gauche) au plus clair (à droite).

Ainsi, l'histogramme d'une image en 256 niveaux de gris sera représenté par un graphique possédant 256 valeurs en abscisses, et le nombre de pixels de l'image en ordonnées. Prenons par exemple cette image en niveaux de gris :

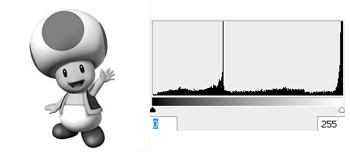
L'histogramme fait apparaître que les tons gris clairs sont beaucoup plus présents dans l'image que les tons foncés.

Pour les images en couleur plusieurs histogrammes sont nécessaires. Par exemple pour une image codée en RGB :

• un histogramme représentant la distribution de la luminance
• trois histogrammes représentant respectivement la distribution des valeurs respectives des composantes rouges, vertes et bleues.

Pourquoi modifier un histogramme et quelles information avoir ?

Lorsque l'on prend une photo, la dynamique des couleurs peut être mal répartie qui peut être lié à une sur/sous-exposition, un contre-jour ou le réglage de l'appareil de prise de vue. Le but de changer l'histogramme d'une image consiste à changer les couleurs pour augmenter le contraste sans faire de saturation.

Cette technique est utilisée dans beaucoup de domaine. Elle est très utile dans le domaine médical où elle trouve un automatisme afin de traiter scanner et autres radio le plus rapidement possible afin de bien voir les détails.

Un histogramme permet d'avoir deux informations sur une image

• Savoir si l'image est sombre ou non. Une image sera sombre lorsque les pics sont sur plus vers la gauche de l'histogramme. Si ils sont vers la droite, l'image va être claire.
• Avoir des informations sur le contraste de l'image : si les pics sont au milieu de l'histogramme, l'image ne sera pas très contrastée. Si ceux-ci sont sur les bords, l'image sera fortement contrastée.

Méthode pour le réhaussement d'image

La méthode pour faire du rehaussement d’image consiste en le calcul de l’histogramme de cette image.

Il existe ensuite différente méthode :

Méthode 1 : Egalisation d'histogramme

L'égalisation d'histogramme a pour but d'harmoniser la répartition des niveaux de luminosité de l'image, de telle manière à tendre vers un même nombre de pixel pour chacun des niveaux de l'histogramme. Cette opération vise à augmenter les nuances dans l'image.

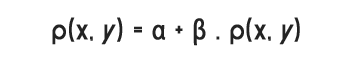
On modifie chaque pixel n lui appliquant une transformation linéaire.

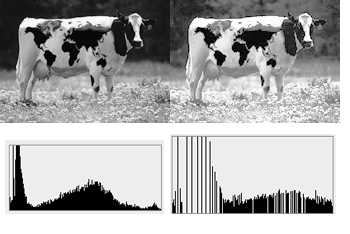
La courbe tonale correspondant à l'égalisation de l'histogramme dépend totalement de l'image. Toutefois la plupart des outils proposent généralement un outil permettant de faire cette opération automatiquement.

Méthode 2 : Linéarisation d'histogramme

L'étirement d'histogramme consiste à répartir les fréquences d'apparition des pixels sur la largeur de l'histogramme. Ainsi il s'agit d'une opération consistant à modifier l'histogramme de telle manière à répartir au mieux les intensités sur l'échelle des valeurs disponibles. Ceci revient à étendre l'histogramme afin que la valeur d'intensité la plus faible soit à zéro et que la plus haute soit à la valeur maximale.

avec P(u) histogramme cumulé.

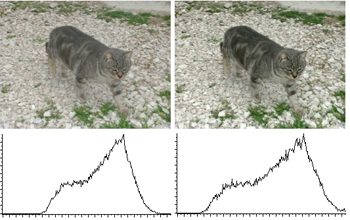
Il est ainsi possible d'augmenter la clarté de l'image par augmentation du contraste. Par exemple une image trop foncée pourra devenir plus "visible". Toutefois cela ne donne pas toujours de bons résultats.

Généralités sur les filtres de convolution

Avant d'entrer dans les détails d'amélioration d'image, il faut savoir que la majorité des traitements sur les images sont basés sur des produits de convolutions.

Comme nous l'avons dit auparavant, nous pouvons résumer une image numérique en un tableau de pixel à deux dimensions où l'on peut retrouver chaque pixel grace à leur valeurs X,Y (coordonnées); on y retouve aussi les informations liées à la luminosité du pixel en question. Dans le langage mathématique, on désigne ce genre de tableau par une matrice sur laquelle on peut faire plusieurs opérations (multiplication, addition, ...)

Un produit de convolution est donc ce qui permet de multiplier deux matrices entre elles.

Dans notre étude, nous multiplierons donc une image avec un filtre qui est souvent une matrice de taille 3*3. La matrice du filtre va donc agir sur chaque pixel de la matrice de l'image.

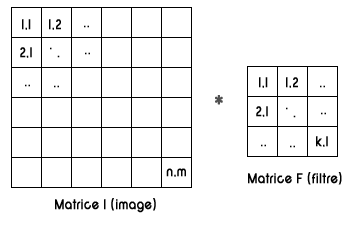
Dans notre exemple ci-dessus, la matrice I de taille n*m représente la matrice de l'image. La matrice F de taille k*l représente le filtre à appliquer sur l'image. Le produit de convolution signifie donc de multiplier chaque pixel de I par F.

Amélioration par filtrage

Il existe deux catégories de filtres :

• filtres linéaires
• filtres morphologique (non linéaire)

Les filtres linéaires

Le filtre passe-haut

Les filtres passe-haut permettent d’accentuer les détails et le contraste, c’st la raison pour laquelle le terme de filtre "d’accentuation" est parfois utilisé.

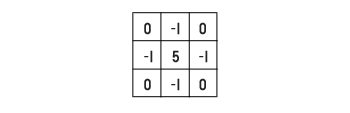
Un filtre passe-haut est composé d'un filtre ayant des valeurs négatives autour d'un pixel central.

Voici une image d'une vue aérienne que nous avons convolué avec un filtre passe-haut.

Nous pouvons voir que l'image de base est assez floue. Ainsi, l'utilisation d'un filtre passe-haut a permit de relever des détails comme les maisons ou les arbres. Mais, en s'attardant plus sur les détails, nous pouvons voir des effets secondaires :

• Augmentation du bruit : ce problème survient surtout sur les parties les plus claires de l'image.
• Effets de bords : parfois, il est possible qu'un cadre survient sur les bords de l'image (sur l'image traitée en bas à droite par exemple). Il peut être corrigé en rognant l'image.

Le filtre passe-bas

Inversement au filtre passe-haut, les filtres passe-bas adoucissent les détails et réduit les bruits granuleux. Il n'est pas en soit (utilisé seul), un élément améliorateur d'image mais couplé au filtre passe-haut, il permet de régler les problèmes de bruit granuleux et ce sans perdre les détails.

Les filtres non-linéaires

Le filtre moyenne et le filtre médian

Ce filtre est un cas particulier du passe-bas, il remplace chaque pixels par la moyenne des pixels voisins et du pixel voisin.

Le filtre médian, quant à lui, atténue les pixels isolés qui ont une valeur très différente de leur entourage.

Le filtre médian est par abus de langage un filtre de convolution. On entend par là qu'il utilise quand même une matrice F de 3*3 mais ensuite, on collecte les 9 élements qu'on range par ordre croissant. Ainsi, la valeur médiane des éléments est celle qui sépare ces élements en deux parties égales. Ainsi, l'algorithme va remplacer la valeur originale par la médiane.

Le résultat que l'on obtient avec ce filtre est qu'il élimine les pixels isolés (par exemple un pixel noir parmi un surface blanche) tout en évitant de faire un flou trop important dans l'image (qui se verrait si c'était le cas)

Le filtre directionnel

Il réhausse les caractéristiques suivant la direction donnée.

Le filtre laplacien

Le filtre Laplacien permet de détecter parfaitement les contours car il évalue les variations d'intensité sur toute la surface à traiter.

Ses plus fréquentes utilisations sont la détection de contour ou la reconnaissance de formes. Il n'est pas à proprement parlé un filtre qui améliore la qualité de l'image numérique à but grand public. En effet, dans des applications plus professionnelles et industrielles, le filtre laplacien a son utilité d'améliorateur d'image dans le sens qu'il peut détecter des formes qu'on ne verrai pas forcement "a l'oeil nu". C'est le cas par exemple en astronimie pour détecter des cercles pour voir des étoiles par exemple.

Nous considérons ainsi que le filtre laplacien est un filtre qui améliore la qualité d'une image numérique dans certains cas.

Le leplacien est une dérivée d'ordre 2 à deux dimensions. Soit I la matrice Image de l'image originale et I(x,y) la position des pixels dans la matrice I, la formule mathématique du laplacien est donc :

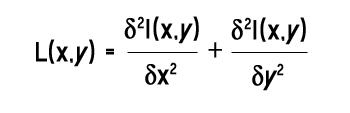
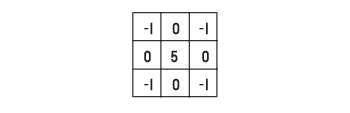
d'où la matrice :

L’image de départ I(x, y) n’est pas une fonction continue(c'est une fonction discrète dûe à la numérisation). Cela dit, on peut quand même avoir une dérivée seconde grâce à trois matrices typiques de taille 3x3

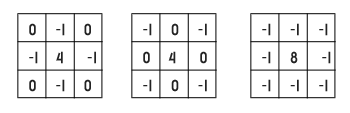
Il faut tout de même noter que la somme de tous les éléments d'une matrice laplacienne vaut toujours zéro. Ce qui montre que laplacien n'est pas un filtre linéaire.

Le seul inconvénient de ce filtre est qu'il fait ressortir le bruit sur les images traitées.

Des scripts et autres programmes

Voici un programme en C sur le rééquilibrage d'histogramme (fichier .zip)

Voici un script Scilab sur le réhaussement d'image (fichier .zip)

Voici un script Scilab sur le lissage (fichier .zip)